ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 10 стр. 113
Условие
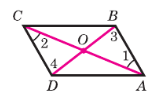
Докажите, что диагонали параллелограмма точкой пересечения делятся пополам.
Решение #1
Пусть О — точка пересечения диагоналей АС и BD параллелограмма ABCD (рис. 159). Треугольники AOB и COD равны по стороне и двум прилежащим углам (AB = CD как противоположные стороны параллелограмма, ∠1 = ∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении параллельных прямых AB и CD секущими АС и BD соответственно). Поэтому АО = ОС и OB = OD, что и требовалось доказать.
Сообщить об ошибке
Сообщитe об ошибке