ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 11 стр. 113
Условие
Сформулируйте и докажите утверждения о признаках параллелограмма.
Решение #1
- Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
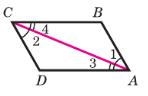
Пусть в четырёхугольнике ABCD стороны AB и CD параллельны и AB = CD (см. рис. 158).
Проведём диагональ АС, разделяющую данный четырёхугольник на два треугольника: ABC и CDA. Эти треугольники равны по двум сторонам и углу между ними (АС — общая сторона, AB = CD по условию, ∠1 = ∠2 как накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС), поэтому ∠3 = ∠4. Но углы 3 и 4 накрест лежащие при пересечении прямых AD и ВС секущей АС, следовательно, AD || BC.
Таким образом, в четырёхугольнике ABCD противоположные стороны попарно параллельны, а значит, четырёхугольник ABCD — параллелограмм.
-
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник — параллелограмм.
Проведём диагональ АС данного четырёхугольника ABCD, разделяющую его на треугольники ABC и CDA (см. рис. 158). Эти треугольники равны по трём сторонам (АС — общая сторона, AB = CD и BC = DA по условию), поэтому ∠1 = ∠2. Отсюда следует, что AB || CD. Так как AB = CD и AB || CD, то по 1 признаку
четырёхугольник ABCD — параллелограмм.
-
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
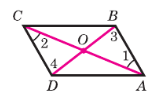
Рассмотрим четырёхугольник ABCD, в котором диагонали АС и BD пересекаются в точке О и делятся этой точкой пополам (см. рис. 159). Треугольники AOB и COD равны по первому признаку равенства треугольников (АО = ОС, BO = OD по условию, ∠AOB = ∠COD как вертикальные углы), поэтому AB = CD и ∠1 = ∠2. Из равенства углов 1 и 2 следует, что AB || CD.
Итак, в четырёхугольнике ABCD стороны AB и CD равны и параллельны, значит, по 1 признаку четырёхугольник ABCD — параллелограмм.
Сообщить об ошибке
Сообщитe об ошибке