ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 11 стр. 88

11 стр. 88

Вернуться к учебнику

Условие

Докажите, что катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Сформулируйте и докажите обратное утверждение.

Решение #1

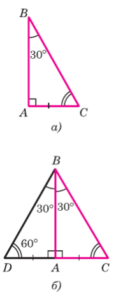
Рассмотрим прямоугольный треугольник ABC, в котором угол A — прямой, ∠B = 30° и, значит, ∠C = 60° (рис. 131, а). Докажем, что AC=1/2BC.

Приложим к треугольнику ABC равный ему треугольник ABD так, как показано на рисунке 131, б. Получим треугольник BCD, в котором ∠B = ∠D = 60°, поэтому DC = BC. Но AC=1/2DC. Следовательно, AC=1/2BC.

Обратное утверждение:

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.

Сообщить об ошибке

Сообщитe об ошибке

Отправить