ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 111 стр. 36
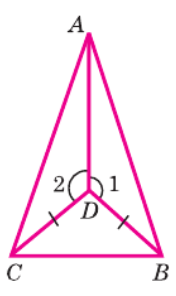
1. Рассмотрим треугольники ADC и ADB.
- CD = BD (это дано по условию, что отмечено на рисунке).
- ∠2 = ∠1 (это дано по условию).
- AD — общая сторона для обоих треугольников.
2. Мы видим, что в треугольниках ADC и ADB есть две пары равных сторон (CD = BD и AD = AD) и равные углы между этими сторонами (∠2 = ∠1).
Следовательно, по первому признаку равенства треугольников (по двум сторонам и углу между ними), треугольник ADC равен треугольнику ADB (ΔADC = ΔADB).
3. Из равенства треугольников ADC и ADB следует равенство их соответствующих сторон. Сторона AC в треугольнике ADC соответствует стороне AB в треугольнике ADB, так как они лежат напротив равных углов (∠2 и ∠1 соответственно).
Значит, AC = AB.
4. По определению, если две стороны треугольника равны, то этот треугольник является равнобедренным. Поскольку мы доказали, что AC = AB, то треугольник ABC является равнобедренным.
Что и требовалось доказать.