ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 112 стр. 37
Условие
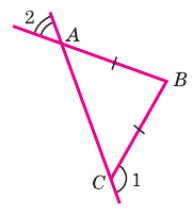
На рисунке 66 AB = ВС, ∠1 = 130°. Найдите ∠2.
Решение #1
1. Найдем внутренний угол при вершине C (∠BCA):
Угол ∠1 и внутренний угол ∠BCA являются смежными (образуют линейную пару), так как они лежат на одной прямой. Сумма смежных углов равна 180°.
∠BCA + ∠1 = 180°
∠BCA + 130° = 180°
∠BCA = 180° — 130°
∠BCA = 50°
2. Найдем угол ∠BAC:
По условию, AB = BC. Это означает, что треугольник ABC является равнобедренным. В равнобедренном треугольнике углы при основании равны. Угол, противолежащий стороне AB, это ∠BCA, а угол, противолежащий стороне BC, это ∠BAC.
Следовательно, ∠BAC = ∠BCA.
Так как ∠BCA = 50°, то ∠BAC = 50°.
3. Найдем угол ∠2:
Угол ∠2 и угол ∠BAC являются вертикальными углами. Вертикальные углы равны.
Следовательно, ∠2 = ∠BAC.
Так как ∠BAC = 50°, то ∠2 = 50°.
Сообщить об ошибке
Сообщитe об ошибке