ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 117 стр. 37

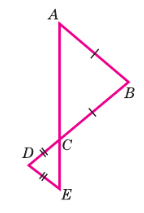
1. Рассмотрим треугольник ABC.

По условию, AB = BC. Так как две стороны равны, треугольник ABC является равнобедренным.

В равнобедренном треугольнике углы, лежащие против равных сторон (углы при основании), равны. Следовательно, ∠BAC = ∠BCA.

2. Рассмотрим треугольник CDE.

По условию, CD = DE. Так как две стороны равны, треугольник CDE является равнобедренным.

В равнобедренном треугольнике углы, лежащие против равных сторон (углы при основании), равны. Следовательно, ∠DCE = ∠CED.

3. Рассмотрим углы при вершине C.

Углы ∠BCA и ∠DCE являются вертикальными углами, так как они образованы пересечением двух прямых (AE и BD).

Вертикальные углы равны. Следовательно, ∠BCA = ∠DCE.

4. Соединяем результаты.

Из пункта 1 мы знаем, что ∠BAC = ∠BCA.

Из пункта 3 мы знаем, что ∠BCA = ∠DCE.

Из пункта 2 мы знаем, что ∠DCE = ∠CED.

Из этих трех равенств следует:

∠BAC = ∠BCA = ∠DCE = ∠CED.

Таким образом, ∠BAC = ∠CED.

Что и требовалось доказать.