ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 122 стр. 40

а)

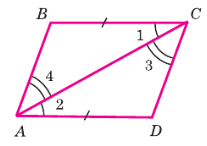
Рассмотрим треугольники △ABC и △CDA.

1. Сторона AC является общей для обоих треугольников.

2. Угол ∠1 (который является ∠BCA в △ABC) равен углу ∠2 (который является ∠DAC в △CDA). Это дано по условию задачи (∠1 = ∠2).

3. Угол ∠4 (который является ∠BAC в △ABC) равен углу ∠3 (который является ∠DCA в △CDA). Это также дано по условию задачи (∠3 = ∠4).

Таким образом, в △ABC и △CDA мы имеем:

∠BCA = ∠DAC (угол)

Общая сторона AC (сторона, прилежащая к этим углам)

∠BAC = ∠DCA (угол)

По второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам), если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Следовательно, △ABC = △CDA.

б) Поскольку мы доказали, что △ABC = △CDA, то их соответствующие стороны и углы равны.
Соответствующие стороны в равных треугольниках:

Сторона AB в △ABC соответствует стороне CD в △CDA (так как они лежат напротив равных углов ∠BCA и ∠DAC соответственно).

Сторона BC в △ABC соответствует стороне AD в △CDA (так как они лежат напротив равных углов ∠BAC и ∠DCA соответственно).

Используя данные нам длины AB = CD и BC = AD, подставим данные значения:

AB = 11 см (так как CD = 11 см)

BC = 19 см (так как AD = 19 см)