ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 124 стр. 40
Условие
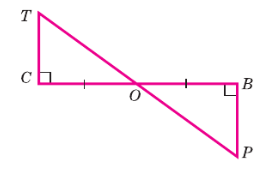
По данным рисунка 73 докажите, что ОР = ОТ, ∠P = ∠T.
Решение #1
Рассмотрим треугольники ΔTOC и ΔPOB.
- ∠TCO = ∠PBO = 90°. Эти углы равны, так как оба являются прямыми углами, указанными на рисунке.
- CO = OB. Это дано по условию, обозначено одинаковыми отметками на отрезках CB.
- ∠TOC = ∠POB. Эти углы являются вертикальными углами, образованными при пересечении прямых TP и CB. Вертикальные углы всегда равны.
Таким образом, на основе признака равенства треугольников по стороне и двум прилежащим к ней углам, мы можем утверждать, что ΔTOC = ΔPOB.
Из равенства треугольников следует равенство их соответствующих сторон и углов:
Соответствующей стороной для TO в ΔTOC является PO в ΔPOB. Следовательно, OP = OT.
Соответствующим углом для ∠T (т.е. ∠CTO) в ΔTOC является ∠P (т.е. ∠BPO) в ΔPOB. Следовательно, ∠P = ∠T.
Что и требовалось доказать.
Сообщить об ошибке
Сообщитe об ошибке