ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 125 стр. 40
Условие
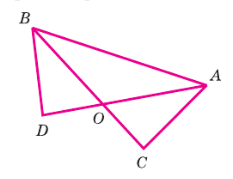
На рисунке 74 ∠DAC = ∠DBC, АО = ВО. Докажите, что ∠C = ∠D и AC = BD.
Решение #1
Рассмотрим треугольники ΔAOC и ΔBOD:
- ∠AOC = ∠BOD. Эти углы являются вертикальными углами, образованными пересечением прямых AB и CD. Вертикальные углы всегда равны.
- AO = BO. Это дано в условии задачи.
- ∠OAC = ∠OBD. Нам дано, что ∠DAC = ∠DBC. Угол ∠OAC является частью угла ∠DAC (точнее, это один и тот же угол, так как точка O лежит на отрезке DC). Угол ∠OBD является частью угла ∠DBC (точнее, это один и тот же угол, так как точка O лежит на отрезке DC). Следовательно, из ∠DAC = ∠DBC вытекает, что ∠OAC = ∠OBD.
Таким образом, мы имеем сторону и два прилежащих к ней угла, равные соответственно стороне и двум прилежащим углам другого треугольника. Поэтому, ΔAOC = ΔBOD.
Из равенства треугольников следует равенство их соответствующих элементов:
1. ∠C = ∠D:
Угол ∠ACO является соответствующим углом для ∠BDO. Так как ΔAOC = ΔBOD, то ∠ACO = ∠BDO. Угол ∠ACO является углом ∠C в контексте всего рисунка. Угол ∠BDO является углом ∠D в контексте всего рисунка. Следовательно, ∠C = ∠D.
2. AC = BD:
Сторона AC является соответствующей стороной для BD. Так как ΔAOC = ΔBOD, то AC = BD. Следовательно, AC = BD.
Что и требовалось доказать.
Сообщить об ошибке
Сообщитe об ошибке