ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 137 стр. 41
Условие
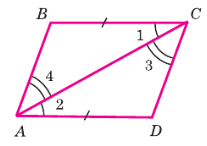
На рисунке 53 (см. с. 31) BC = AD, AB = CD. Докажите, что ∠B = ∠D.
Решение #1
Рассмотрим два треугольника: ΔABC и ΔCDA:
- AB = CD (дано по условию).
- BC = AD (дано по условию).
- AC = CA (общая сторона для обоих треугольников).
Поскольку все три стороны треугольника ABC равны соответствующим трем сторонам треугольника CDA (AB=CD, BC=AD, AC=CA), то эти треугольники равны по третьему признаку равенства треугольников (по трем сторонам). Следовательно, ΔABC = ΔCDA.
Из равенства треугольников следует равенство их соответствующих углов.
Угол B в треугольнике ABC лежит напротив стороны AC.
Угол D в треугольнике CDA лежит напротив стороны AC.
Так как AC является общей стороной, углы, лежащие напротив этой стороны в равных треугольниках, также равны.
Следовательно, ∠B = ∠D.
Что и требовалось доказать.
Сообщить об ошибке
Сообщитe об ошибке