ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 139 стр. 41
Условие
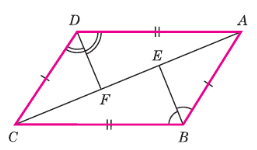
На рисунке 76 AB = CD, AD = ВС, BE — биссектриса угла ABC, a DF — биссектриса угла ADC. Докажите, что:
а) ∠ABE = ∠ADF;
б) ΔABE = ΔCDF.
Решение #1
a)
1. BE — биссектриса угла ABC, следовательно, ∠ABE = ∠ABC/2.
DF — биссектриса угла ADC, следовательно, ∠ADF = ∠ADC/2.
2. В параллелограмме ABCD противолежащие углы равны, то есть ∠ABC = ∠ADC.
3. Подставим значение ∠ADC в уравнение для ∠ADF:
∠ADF = ∠ABC/2 = ∠ABE.
Следовательно, ∠ABE = ∠ADF.
б)
1. Мы имеем два треугольника: ΔABE и ΔCDF, для которых:
AB = CD (по условию задачи),
AD = BC (по условию задачи),
∠ABE = ∠ADF (доказали выше).
По двум сторонам и углу между ними треугольники равны: ΔABE = ΔCDF.
Сообщить об ошибке
Сообщитe об ошибке