ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 14 стр. 184
Условие
Сформулируйте и докажите теорему об отрезках пересекающихся хорд.
Решение #1
Теорема:
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство:
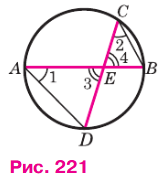
Пусть хорды AB и CD пересекаются в точке Е (рис. 221). Докажем, что
AE ⋅ BE = CE ⋅ DE.
Рассмотрим треугольники ADE и СВЕ. В этих треугольниках углы 1 и 2 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 3 и 4 равны как вертикальные. По первому признаку подобия треугольников ΔADE~ΔCBE. Отсюда следует, что AE/CE=DE/BE, или AE ⋅ BE = CE ⋅ DE. Теорема доказана.
Сообщить об ошибке
Сообщитe об ошибке