ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 15 стр. 114
Условие
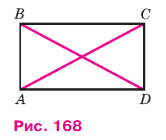
Докажите, что если в параллелограмме диагонали равны, то параллелограмм является прямоугольником.
Решение #1
Пусть в параллелограмме ABCD диагонали АС и BD равны (см. рис. 168). Треугольники ABD и DCA равны по трём сторонам (AB = DC, BD = CA, AD — общая сторона). Отсюда следует, что ∠A = ∠D. Так как в параллелограмме противоположные углы равны, то ∠A = ∠C и ∠B = ∠D. Таким образом, ∠A = ∠B = ∠C = ∠D. Параллелограмм — выпуклый четырёхугольник, поэтому ∠A + ∠B + ∠C + ∠D = 360°. Следовательно, ∠A = ∠B = ∠C = ∠D = 90°, т. е. параллелограмм ABCD является прямоугольником.
Сообщить об ошибке
Сообщитe об ошибке