ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 15 стр. 185

15 стр. 185

Вернуться к учебнику

Условие

Сформулируйте и докажите теорему о биссектрисе угла.

Решение #1

Теорема:

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

Доказательство:

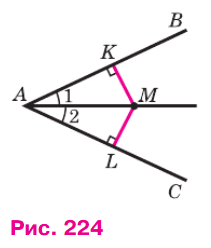
Возьмём произвольную точку М на биссектрисе угла ВАС, проведём перпендикуляры МK и ML к прямым AB и АС и докажем, что MK = ML (рис. 224). Рассмотрим прямоугольные треугольники АМK и AML. Они равны по гипотенузе и острому углу (AM — общая гипотенуза, ∠1 = ∠2 по условию). Следовательно, MK = ML.

Сообщить об ошибке

Сообщитe об ошибке

Отправить