ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 16 стр. 185
Условие
Докажите, что биссектрисы треугольника пересекаются в одной точке.
Решение #1
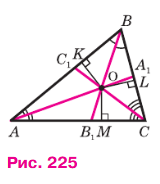
В самом деле, обозначим буквой О точку пересечения биссектрис АА1 и BB1 треугольника ABC и проведём из этой точки перпендикуляры OK, OL и OM соответственно к прямым AB, ВС и СА (рис. 225). По доказанной теореме ОK = OM и OK = OL. Поэтому OM = OL, т. е. точка О равноудалена от сторон угла АСВ и, значит, лежит на биссектрисе CC1 этого угла. Следовательно, все три биссектрисы треугольника ABC пересекаются в точке О, что и требовалось доказать.
Сообщить об ошибке
Сообщитe об ошибке