ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 16 стр. 67

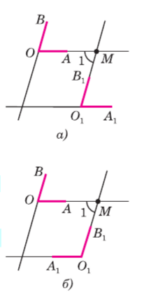
Пусть ∠AOB и ∠А1О1В1 — данные углы и OA || O1A1, OB || O1B1. Если угол AOB развёрнутый, то и угол А1О1В1 — развёрнутый (объясните почему), поэтому эти углы равны. Пусть ∠AOB — неразвёрнутый угол. Возможные случаи расположения углов AOB и А1О1В1 изображены на рисунке, а и б. Прямая О1В1 пересекает прямую О1А1 и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М. Параллельные прямые ОВ и О1В1 пересечены секущей OM, поэтому один из углов, образованных при пересечении прямых О1В1 и ОА (угол 1 на рисунке), равен углу AOB (как накрест лежащие углы).

Параллельные прямые ОА и O1A1 пересечены секущей О1М, поэтому либо ∠1 = ∠A1O1B1 (рис., а), либо ∠1 + ∠A1O1B1= 180° (рис., б). Из равенства ∠1 = ∠AOB и последних двух равенств следует, что либо ∠AOB = ∠A1O1B1 (см. рис., а), либо ∠AOB + ∠A1O1B1= 180° (см. рис., б). Теорема доказана.