ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 162 стр. 49

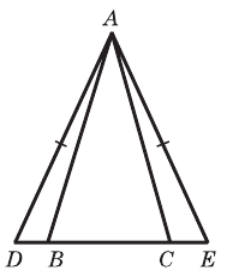
а)

1. Рассмотрим треугольники ΔABD и ΔACE.

• AD = AE (как боковые стороны равнобедренного ΔADE).
• BD = CE (дано по условию).
• ∠ADB = ∠AEC (или ∠D = ∠E, как углы при основании равнобедренного ΔADE).

Следовательно, ΔABD = ΔACE по первому признаку равенства треугольников (по двум сторонам и углу между ними).

2. Из равенства ΔABD = ΔACE следуют равенства соответствующих элементов:

• AB = AC (как соответствующие стороны равных треугольников).
• ∠BAD = ∠CAE (как соответствующие углы равных треугольников).

3. Докажем, что ∠CAD = ∠BAE.

Угол ∠DAE можно представить как сумму углов:

∠DAE = ∠DAB + ∠BAC + ∠CAE.

Рассмотрим ∠CAD = ∠DAE — ∠CAE и ∠BAE = ∠DAE — ∠DAB.

Так как мы доказали, что ∠DAB = ∠CAE, то отнимая равные углы от одного и того же угла ∠DAE, мы получаем равные результаты. Значит, ∠CAD = ∠BAE.

б)

1. Обозначим углы: пусть ∠CAD = ∠BAE = x (по условию) и ∠BAC = y.

2. Выразим углы ∠DAB и ∠CAE.

Угол ∠DAE можно записать как сумму:

∠DAE = ∠DAB + ∠BAE.

Давайте выразим ∠DAB и ∠CAE через x и общий угол ∠DAE.

∠DAB = ∠DAE — ∠BAE.

∠CAE = ∠DAE — ∠CAD.

Так как ∠CAD = ∠BAE (по условию), то ∠DAE — ∠BAE = ∠DAE — ∠CAD. Следовательно, ∠DAB = ∠CAE.

3. Рассмотрим треугольники ΔABD и ΔACE:

• AD = AE (как боковые стороны равнобедренного ΔADE).
• ∠ADB = ∠AEC (или ∠D = ∠E, как углы при основании равнобедренного ΔADE).
• ∠DAB = ∠CAE (доказано выше).

Следовательно, ΔABD = ΔACE по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам).

4. Из равенства ΔABD = ΔACE следуют равенства соответствующих элементов:

• BD = CE (как соответствующие стороны равных треугольников).
• AB = AC (как соответствующие стороны равных треугольников).