ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 164 стр. 50

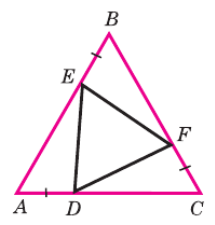
1. Рассмотрим углы внешнего треугольника:

Поскольку треугольник ABC — равносторонний, все его углы равны 60 градусам. Следовательно, ∠A = ∠B = ∠C = 60°.

2. Поскольку треугольник ABC — равносторонний, все его стороны равны. Пусть длина стороны AB = BC = CA = s.

3. Рассмотрим треугольники, окружающие треугольник DEF:

Нам нужно доказать равенство сторон DE, EF, FD. Для этого рассмотрим треугольники ΔADE, ΔBEF и ΔCFD. Для ΔADE и ΔBEF и ΔCFD:

• По условию дано, что AD = BE = CF. Это первая пара равных сторон для наших треугольников.
• Как было установлено в пункте 1, ∠A = ∠B = ∠C = 60°. Эти углы являются углами между сторонами, которые мы рассматриваем (например, для ΔADE это угол между сторонами AD и AE).
• Теперь найдем длины оставшихся сторон этих треугольников: AE, BF, CD.

AE = AB — BE. Так как AB = s и BE = AD (по условию), то AE = s — AD.

BF = BC — CF. Так как BC = s и CF = AD (по условию), то BF = s — AD.

CD = CA — AD. Так как CA = s и AD = AD, то CD = s — AD.

Из этого следует, что AE = BF = CD.

Таким образом, по первому признаку равенства треугольников (по двум сторонам и углу между ними), треугольники ΔADE, ΔBEF и ΔCFD равны: ΔADE = ΔBEF = ΔCFD.

4. Из равенства треугольников следует равенство их соответствующих сторон. Стороны DE, EF и FD являются сторонами, лежащими напротив равных углов (60°) в этих равных треугольниках.
Следовательно, DE = EF = FD.

Так как все три стороны треугольника DEF равны, то треугольник DEF является равносторонним.

Что и требовалось доказать.