ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 17 стр. 67

Формулировка теоремы:

Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы равны или в сумме составляют 180∘.

Доказательство:

Пусть ∠АОВ и ∠А1О1В1 — данные углы, ОА ⊥ О1А1, ОВ ⊥ О1В1. Если угол AOB развёрнутый или прямой, то и угол А1О1В1 развёрнутый или прямой (объясните почему), поэтому эти углы равны. Пусть ∠AOB < 180°, О ∉ O1A1, О ∉ O1B1 (случаи О ∈ O1A1, O ∈ O1B1 рассмотрите самостоятельно).

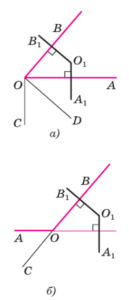
Возможны два случая (рис.).

1⁰. ∠AOB < 90° (см. рис., а). Проведём луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными, а точки В и С лежали по разные стороны от прямой ОА. Далее, проведём луч OD так, чтобы прямые ОВ и OD были взаимно перпендикулярными, а точки С и D лежали по одну сторону от прямой ОА. Поскольку ∠AOB = 90° − ∠AOD и ∠COD = 90° − ∠AOD, то ∠AOB = ∠COD. Стороны угла COD соответственно параллельны сторонам угла A1O1B1 (объясните почему), поэтому либо ∠COD = ∠A1O1B1, либо ∠COD + ∠A1O1B1 = 180°. Следовательно, либо ∠AOB = ∠A1О1В1, либо ∠AOB + ∠A1O1B1 = 180°.

2⁰. ∠AOB > 90° (см. рис., б). Проведём луч ОС так, чтобы угол АОС был смежным с углом AOB. Угол АОС острый, и его стороны соответственно перпендикулярны сторонам угла А1О1В1. Следовательно, либо ∠AOC + ∠A1O1B1 = = 180°, либо ∠АОС = ∠A1O1B1. В первом случае ∠AOB = ∠А1О1В1, во втором случае ∠AOB + + ∠A1O1B1 = 180°. Теорема доказана.