ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 18 стр. 185

18 стр. 185

Вернуться к учебнику

Условие

Сформулируйте и докажите теорему о серединном перпендикуляре к отрезку.

Решение #1

Теорема:

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Доказательство:

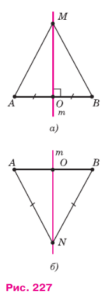
Пусть прямая m — серединный перпендикуляр к отрезку AB, точка О — середина этого отрезка (рис. 227, а).

Рассмотрим произвольную точку М прямой m и докажем, что АМ = ВМ. Если точка М совпадает с точкой О, то это равенство верно, так как О — середина отрезка AB. Пусть М и О — различные точки. Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ, OM — общий катет), поэтому AM = ВМ.

Сообщить об ошибке

Сообщитe об ошибке

Отправить