ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 186 стр. 56

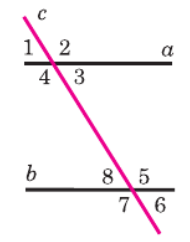
Давайте определим типы углов по рисунку 106:

• Накрест лежащие внутренние углы: ∠3 и ∠8; ∠4 и ∠5.
• Соответственные углы: ∠1 и ∠8; ∠2 и ∠5; ∠4 и ∠7; ∠3 и ∠6.
• Односторонние внутренние углы: ∠3 и ∠5; ∠4 и ∠8.
• Накрест лежащие внешние углы: ∠1 и ∠6; ∠2 и ∠7.
• Односторонние внешние углы: ∠1 и ∠7; ∠2 и ∠6.
• Вертикальные углы: ∠1 и ∠3; ∠2 и ∠4; ∠5 и ∠7; ∠8 и ∠6.
• Смежные углы (образующие развернутый угол): ∠1 и ∠2; ∠2 и ∠3; ∠3 и ∠4; ∠4 и ∠1; ∠8 и ∠5; ∠5 и ∠6; ∠6 и ∠7; ∠7 и ∠8.

Теперь рассмотрим каждый случай:

а) ∠1 = 37°, ∠7 = 143°

1. Углы ∠1 и ∠7 являются односторонними внешними углами.

2. Найдем их сумму: ∠1 + ∠7 = 37° + 143° = 180°.

3. Признак параллельности: если сумма односторонних внешних углов, образованных при пересечении двух прямых секущей, равна 180°, то прямые параллельны.

4. Так как ∠1 + ∠7 = 180°, то прямые a || b.

б) ∠1 = ∠6

1. Углы ∠1 и ∠6 являются накрест лежащими внешними углами.

2. Признак параллельности: если накрест лежащие внешние углы, образованные при пересечении двух прямых секущей, равны, то прямые параллельны.

3. Так как дано, что ∠1 = ∠6, то прямые a || b.

в) ∠1 = 45°, а угол 7 в три раза больше угла 3.

1. Углы ∠1 и ∠3 являются вертикальными углами. По свойству вертикальных углов, они равны, поэтому ∠3 = ∠1 = 45°.

2. Дано: ∠7 = 3 * ∠3. Подставим значение ∠3: ∠7 = 3 * 45° = 135°.

3. Итак, мы имеем ∠1 = 45° и ∠7 = 135°.

4. Углы ∠1 и ∠7 являются односторонними внешними углами.

5. Найдем их сумму: ∠1 + ∠7 = 45° + 135° = 180°.

6. Признак параллельности: если сумма односторонних внешних углов, образованных при пересечении двух прямых секущей, равна 180°, то прямые параллельны.

7. Так как ∠1 + ∠7 = 180°, то прямые a || b.