ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 189 стр. 56

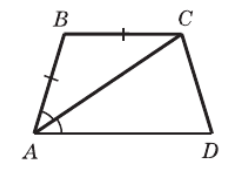
1. Рассмотрим треугольник ABC.

По условию (из рисунка), стороны AB и BC равны (AB = BC).

Если в треугольнике две стороны равны, то этот треугольник является равнобедренным. Значит, ΔABC – равнобедренный с основанием AC.

2. В равнобедренном треугольнике углы при основании равны. В ΔABC основанием является AC, поэтому углы, прилегающие к основанию, равны: ∠BCA = ∠BAC.

3. По условию (из рисунка), углы ∠BAC и ∠CAD равны (∠BAC = ∠CAD).

4. Из пункта 2 мы знаем, что ∠BCA = ∠BAC.

Из пункта 3 мы знаем, что ∠BAC = ∠CAD.

Из этих двух равенств следует, что ∠BCA = ∠CAD.

5.

Прямые BC и AD пересечены секущей AC.

Углы ∠BCA и ∠CAD являются накрест лежащими углами относительно этих прямых и секущей. Мы доказали, что эти накрест лежащие углы равны (∠BCA = ∠CAD).

По признаку параллельности прямых, если накрест лежащие углы, образованные при пересечении двух прямых третьей секущей, равны, то эти прямые параллельны.

Следовательно, BC || AD.

Что и требовалось доказать.