ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 19 стр. 185
Условие
Докажите, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Решение #1
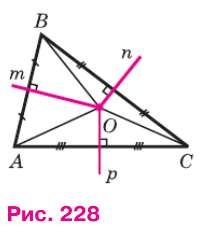
Для доказательства этого утверждения рассмотрим серединные перпендикуляры m и n к сторонам AB и ВС треугольника ABC (рис. 228).
Эти прямые пересекаются в некоторой точке О. В самом деле, если предположить противное, т. е. что m || n, то прямая ВА, будучи перпендикулярной к прямой m, была бы перпендикулярна и к параллельной ей прямой n, а тогда через точку В проходили бы две прямые ВA и BС, перпендикулярные к прямой n, что невозможно.
По доказанной теореме ОВ = ОА и ОВ = ОС. Поэтому ОА = ОС, т. е. точка О равноудалена от концов отрезка АС и, значит, лежит на серединном перпендикуляре р к этому отрезку. Следовательно, все три серединных перпендикуляра m, n и р к сторонам треугольника ABC пересекаются в точке О.
Сообщить об ошибке
Сообщитe об ошибке