ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 190 стр. 56

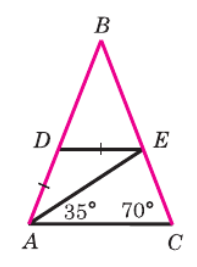
Для доказательства того, что DE || AC, нам нужно показать, что внутренние накрест лежащие углы равны, например, ∠DEA = ∠EAC.

1. Рассмотрим треугольник ABC:

Нам дано, что AB = BC. Это означает, что треугольник ABC является равнобедренным.

В равнобедренном треугольнике углы при основании равны. Следовательно, ∠BAC = ∠BCA.

Нам дано, что ∠C = 70°.

Таким образом, ∠BAC = 70°.

2. Найдем угол ∠DAE (или ∠BAE):

Мы знаем, что ∠BAC = 70°.

Нам дано, что ∠EAC = 35°.

Угол ∠DAE (который является частью ∠BAC) равен:

∠DAE = ∠BAC — ∠EAC = 70° — 35° = 35°

3. Рассмотрим треугольник ADE:

Нам дано, что AD = DE. Это означает, что треугольник ADE является равнобедренным.

В равнобедренном треугольнике углы при основании, противолежащие равным сторонам, равны. Следовательно, ∠DAE = ∠DEA.

Из предыдущего шага мы знаем, что ∠DAE = 35°.

Таким образом, ∠DEA = 35°.

4. Сравним углы:

Мы нашли, что ∠DEA = 35°. Нам дано, что ∠EAC = 35°. Следовательно, ∠DEA = ∠EAC.

5. Углы ∠DEA и ∠EAC являются внутренними накрест лежащими углами при пересечении прямых DE и AC секущей AE. Поскольку эти углы равны (оба равны 35°), прямые DE и AC параллельны.

Что и требовалось доказать.