ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 20 стр. 185

Теорема:

Доказательство:

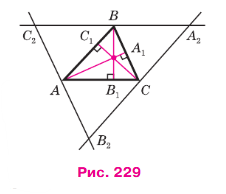
Рассмотрим произвольный треугольник ABC и докажем, что прямые AA1, BB1 и CC1, содержащие его высоты, пересекаются в одной точке (рис. 229).

Проведём через каждую вершину треугольника ABC прямую, параллельную противоположной стороне. Получим треугольник А2В2С2. Точки А, В и С являются серединами сторон этого треугольника. Действительно, AB = А2С и AB = СВ2 как противоположные стороны параллелограммов ABА2С и ABСВ2, поэтому А2С = СВ2. Аналогично С2А = AB2 и С2В = ВА2. Кроме того, как следует из построения, СС1 ⊥ А2В2, АА1 ⊥ В2С2 и ВВ1 ⊥ А2C2. Таким образом, прямые AA1, BB1 и СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2. Поэтому они пересекаются в одной точке. Теорема доказана.