ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 200 стр. 65

Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Если две прямые не параллельны, они обязательно пересекаются.

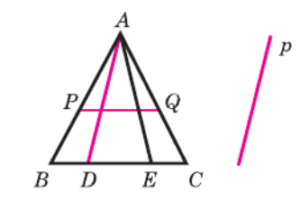
1. Пересечение прямой p с прямыми AB, AE, AC:

Для прямой AB:

Прямые AD и AB проходят через общую точку A.

Мы знаем, что AD || p.

Если бы AB была параллельна p, то через точку A (которая не лежит на p, так как AD и p параллельны и AD не является прямой p по условию) проходили бы две различные прямые (AD и AB), параллельные p.

Однако, согласно аксиоме о параллельных прямых, через точку A можно провести только одну прямую, параллельную p.

Так как AD и AB — это разные прямые (точка D лежит на BC, а не на AB, иначе треугольник ABC был бы вырожденным), это противоречит аксиоме.

Следовательно, прямая AB не параллельна p.

Поскольку AB не параллельна p, они должны пересекаться.

Для прямой AE:

Аналогично, прямые AD и AE проходят через точку A.

AD || p.

Если бы AE была параллельна p, то через точку A проходили бы две различные прямые (AD и AE), параллельные p. Это противоречит аксиоме, так как AD и AE — разные прямые (точка E лежит на BC, а не на AE).

Следовательно, прямая AE не параллельна p, и они должны пересекаться.

Для прямой AC:

Аналогично, прямые AD и AC проходят через точку A.

AD || p.

Если бы AC была параллельна p, то через точку A проходили бы две различные прямые (AD и AC), параллельные p. Это противоречит аксиоме, так как AD и AC — разные прямые (точка D лежит на BC, а не на AC).

Следовательно, прямая AC не параллельна p, и они должны пересекаться.

2. Пересечение прямой p с прямой BC:

Мы знаем, что AD || p.

Прямая BC пересекает прямую AD в точке D.

Предположим, что прямая BC параллельна p.

Тогда через точку D (которая не лежит на p, так как AD и p параллельны) проходили бы две различные прямые (AD и BC), параллельные p.

Это противоречит аксиоме о параллельных прямых (поскольку AD и BC не являются одной и той же прямой).

Следовательно, прямая BC не параллельна p.

Поскольку BC не параллельна p, они должны пересекаться.

3. Пересечение прямой p с прямой PQ:

Мы знаем, что PQ || BC (дано).

Мы только что доказали, что прямая p пересекает прямую BC.

Предположим, что прямая PQ параллельна p.

Если PQ || p и PQ || BC, то согласно тому, что, если две прямые параллельны третьей, то они параллельны между собой, мы получаем, что BC || p.

Однако это противоречит нашему предыдущему выводу о том, что BC пересекает p (то есть BC не параллельна p).

Следовательно, наше предположение, что PQ параллельна p, неверно.

Поскольку PQ не параллельна p, они должны пересекаться.

На основании аксиомы о параллельных прямых и данных условий, прямая p пересекает все указанные прямые: AB, AE, AC, BC и PQ.