ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 202 стр. 65

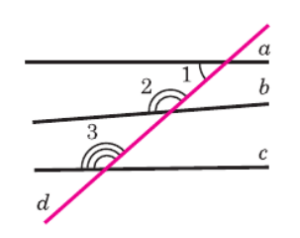
1. Прямые a и b:

У нас есть ∠1 = 42° (на прямой а) и ∠2 = 140° (на прямой b).

Найдем угол, смежный с ∠1 на прямой а, который находится внутри между a и b, слева от секущей d.

Пусть это будет ∠x.

∠x = 180° — ∠1 = 180° — 42° = 138°.

Теперь рассмотрим углы ∠x и ∠2. Они являются односторонними внутренними углами относительно прямых a и b и секущей d.

Если прямые a и b параллельны, то ∠x + ∠2 должно быть равно 180°.

138° + 140° = 278°

Так как 278° ≠ 180°, прямые a и b не параллельны.

2. Прямые b и c:

У нас есть ∠2 = 140° (на прямой b) и ∠3 = 138° (на прямой c).

∠2 и ∠3 являются односторонними внутренними углами относительно прямых b и c и секущей d (они оба находятся слева от d и между прямыми b и c).

Если прямые b и c параллельны, то ∠2 + ∠3 должно быть равно 180°.

140° + 138° = 278°

Так как 278° ≠ 180°, прямые b и c не параллельны.

3. Прямые a и c:

У нас есть ∠1 = 42° (на прямой а) и ∠3 = 138° (на прямой c).

Найдем угол, смежный с ∠1, который находится внутри между a и c, справа от секущей d. Пусть это будет ∠y.

∠y = 180° — ∠1 = 180° — 42° = 138°.

Теперь рассмотрим углы ∠y и ∠3.

∠y находится между прямыми a и c, справа от секущей d.

∠3 находится между прямыми a и c, слева от секущей d.

Эти углы являются накрест лежащими внутренними углами.

Если прямые a и c параллельны, то накрест лежащие внутренние углы должны быть равны.
У нас ∠y = 138° и ∠3 = 138°.

Так как 138° = 138°, прямые a и c параллельны.