ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 209 стр. 66

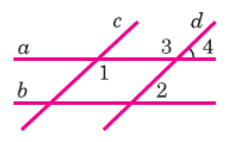
1. Найдем ∠3:

Углы ∠3 и ∠4 являются смежными углами, лежащими на прямой a. Сумма смежных углов равна 180°.

∠3 + ∠4 = 180°

∠3 + 45° = 180°

∠3 = 180° — 45°

∠3 = 135°

2. Найдем ∠2:

Углы ∠4 и ∠2 являются соответственными углами при параллельных прямых a и b и секущей d. Соответственные углы равны.

Так как a || b, то ∠2 = ∠4.

∠2 = 45°

3. Найдем ∠1:

Для того чтобы найти ∠1, необходимо предположить, что прямые c и d также параллельны (c || d). Это типично для таких задач, когда на рисунке линии выглядят параллельными, и требуется найти углы, связанные с обеими парами секущих.

Если c || d, то рассмотрим прямую a как секущую для этих двух параллельных прямых.

Угол ∠3 (135°) и угол, находящийся в том же положении относительно прямой a и секущей c, как ∠3 относительно a и d (то есть, угол, смежный с ∠1 и расположенный справа от c), являются соответственными углами.

Если a || b и c || d, то фигура, образованная пересечением этих линий, является параллелограммом.

Рассмотрим угол, который является внутренним односторонним с ∠1 по отношению к секущей a и параллельным прямым c и d. Этот угол находится на линии a, внутри между c и d, и смежен с ∠3. Пусть это будет угол ∠x.

∠x = ∠4 = 45° (поскольку ∠x и ∠4 — соответственные углы при c || d и секущей a — нет, это не так просто).

Давайте используем более прямое свойство, если c || d:

Рассмотрим прямую a как секущую для параллельных прямых c и d.

Угол ∠3 и угол, соответственный ему при пересечении a и c, будут равны. (Не ∠1 напрямую).

Угол, который является внутренним односторонним с ∠3 относительно секущей a и параллельных c и d, будет равен 180° — 135° = 45°. Пусть это будет угол справа от ∠1 на линии a.

∠1 и этот угол (45°) являются смежными углами на прямой a.

∠1 + 45° = 180°

∠1 = 180° — 45°

∠1 = 135°