ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 210 стр. 66

1. Проведем вспомогательную прямую:

По указанию, рассмотрим продолжение луча CP3 вверх. Обозначим это продолжение как прямую CD, где D — точка выше C на этой вертикальной линии. Прямая CD является вертикальной линией, проходящей через точку C.

2. Параллельность линий:

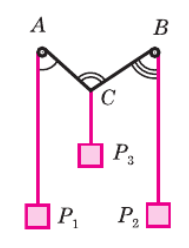
Участок нити AP1 (с грузом P1) висит строго вертикально. Следовательно, прямая, проходящая через AP1, является вертикальной.

Участок нити BP2 (с грузом P2) висит строго вертикально. Следовательно, прямая, проходящая через BP2, является вертикальной.

Участок нити CP3 (с грузом P3) висит строго вертикально. Следовательно, прямая CD, являющаяся продолжением CP3, также является вертикальной.

Так как все эти линии (AP1, BP2, CD) являются вертикальными, они параллельны друг другу.

3. Углы между параллельными прямыми и секущими:

Рассмотрим прямые AP1 и CD как две параллельные прямые, пересеченные секущей AC.

Угол ∠CAP1 (обозначенный одной дугой на рисунке) — это угол между вертикальной прямой AP1 и секущей AC.

Угол ∠ACD (угол между секущей AC и вертикальной прямой CD) является внутренним накрест лежащим углом к ∠CAP1.

По свойству параллельных прямых и секущей, внутренние накрест лежащие углы равны. Следовательно, ∠ACD = ∠CAP1.

Рассмотрим прямые BP2 и CD как две параллельные прямые, пересеченные секущей BC.

Угол ∠CBP2 (обозначенный тремя дугами на рисунке) — это угол между вертикальной прямой BP2 и секущей BC.

Угол ∠BCD (угол между секущей BC и вертикальной прямой CD) является внутренним накрест лежащим углом к ∠CBP2.

По свойству параллельных прямых и секущей, внутренние накрест лежащие углы равны.

Следовательно, ∠BCD = ∠CBP2.

4.

Угол ∠ACB (обозначенный двумя дугами на рисунке) образован отрезками AC и BC. Из рисунка видно, что вертикальная линия CD проходит между этими отрезками.

Таким образом, угол ∠ACB является суммой углов ∠ACD и ∠BCD:

∠ACB = ∠ACD + ∠BCD.

5.

Подставляя равенства, полученные в пункте 3:

∠ACB = ∠CAP1 + ∠CBP2.

Что и требовалось доказать.