ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 213 стр. 67
Условие
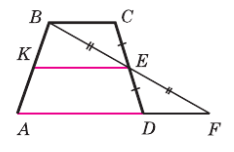
На рисунке 122 CE = ED, BE = EF и KE || AF. Докажите, что KE || ВС.
Решение #1
1. Рассмотрим треугольники BCE и DEF.
- CE = ED (дано)
- BE = EF (дано)
- Углы ∠BEC и ∠DEF являются вертикальными углами, следовательно, они равны: ∠BEC = ∠DEF.
2. По признаку равенства треугольников по двум сторонам и углу между ними, треугольник BCE равен треугольнику DEF (ΔBCE = ΔDEF).
3. Из равенства треугольников следует равенство их соответствующих углов. В частности, ∠BCE = ∠FDE.
4. Рассмотрим прямые BC и AF и секущую CD. Углы ∠BCE и ∠FDE являются накрест лежащими углами при этих прямых и секущей.
5. Так как накрест лежащие углы равны (∠BCE = ∠FDE), это означает, что прямые BC и AF параллельны: BC || AF.
6. Нам также дано, что KE || AF.
7. Если две прямые (BC и KE) параллельны третьей прямой (AF), то они параллельны между собой.
8. Следовательно, KE || BC.
Что и требовалось доказать.
Сообщить об ошибке
Сообщитe об ошибке