ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 247 стр. 74

а)

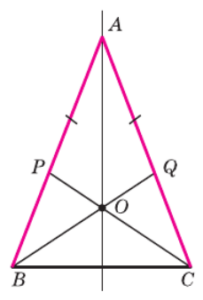
1. Рассмотрим треугольники ABQ и ACP:

• AB = AC (дано, так как треугольник ABC — равнобедренный).
• AP = AQ (дано).
• Угол ∠BAC — общий для обоих треугольников.

2. Следовательно, треугольник ABQ равен треугольнику ACP (по двум сторонам и углу между ними — признак).

3. Из равенства треугольников ABQ и ACP вытекает равенство их соответствующих углов: ∠ABQ = ∠ACP.

4. Обратим внимание на треугольник BOC:

Угол ∠ABQ — это тот же самый угол, что и ∠OBC.

Угол ∠ACP — это тот же самый угол, что и ∠OCB.

Таким образом, мы доказали, что ∠OBC = ∠OCB.

5. Поскольку в треугольнике BOC два угла равны (∠OBC = ∠OCB), то этот треугольник является равнобедренным (по признаку равнобедренного треугольника).

б)

1. Докажем, что треугольник BOC — равнобедренный.

В треугольнике ABC AB = AC (дано). Следовательно, это равнобедренный треугольник, и углы при его основании равны: ∠ABC = ∠ACB.

Мы знаем из предварительного доказательства, что ∠ABQ = ∠ACP.

Рассмотрим углы ∠OBC и ∠OCB:

∠OBC = ∠ABC — ∠ABQ.

∠OCB = ∠ACB — ∠ACP.

Поскольку ∠ABC = ∠ACB и ∠ABQ = ∠ACP, то, вычитая равные величины из равных, получаем: ∠OBC = ∠OCB.

Если в треугольнике BOC углы при основании BC равны, то этот треугольник является равнобедренным.

Следовательно, BO = OC.

2. Рассмотрим треугольник BOA и треугольник COA:

AO – общая сторона для обоих треугольников.

BO = OC (доказано в пункте 1).

AB = AC (дано).

Следовательно, треугольник BOA равен треугольнику COA по трем сторонам (признак равенства треугольников).

3. Из равенства треугольников BOA и COA следует, что AO — биссектриса угла A.

По определению равных треугольников, их соответствующие углы равны.

Таким образом, ∠BAO = ∠CAO (или ∠OAC).

Это означает, что прямая AO является биссектрисой угла A в треугольнике ABC.

4. AO пересекает BC в точке H. Докажем, что AH — высота и медиана.

Пусть прямая AO пересекает основание BC в точке H.

Треугольник ABC является равнобедренным (AB = AC).

Известно свойство равнобедренного треугольника: биссектриса, проведенная из вершины к основанию, одновременно является медианой и высотой, проведенной к этому основанию.

Поскольку AH (часть прямой AO) является биссектрисой угла A в равнобедренном треугольнике ABC, то:

AH перпендикулярна BC (AH ⊥ BC), т.е. AH является высотой.

H является серединой BC (BH = HC), т.е. AH является медианой.