ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 3 стр. 7

Для решения задачи проведем три прямые на плоскости так, чтобы каждая пара из них пересекалась.

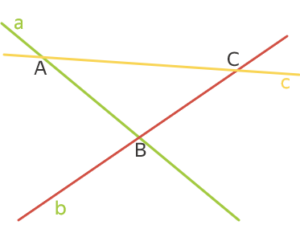
Обозначим три прямые как a, b и c. Проведем их так, чтобы они не были параллельны и не пересекались в одной точке.

Прямая a пересекает прямую b в точке B.

Прямая a пересекает прямую c в точке A.

Прямая b пересекает прямую c в точке C.

Таким образом, у нас есть три точки пересечения: A, B и C.

Каждая пара из трех прямых пересекается в одной уникальной точке, что дает нам общее количество точек пересечения:

$$\text{Количество точек}=3.$$

Возможные случаи

• Все три прямые пересекаются так, как описано выше, образуя три уникальные точки пересечения.
• Если хотя бы две из трех прямых совпадают (например, если прямая a совпадает с прямой b), то у нас будет только одна точка пересечения между ними и одна дополнительная точка от третьей прямой. В этом случае мы получим только две уникальные точки.
• Если все три прямые совпадают, то у нас будет только одна точка пересечения.