ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 4 стр. 184
Условие
Сформулируйте и докажите теорему о свойстве касательной.
Решение #1
Теорема:
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Доказательство:
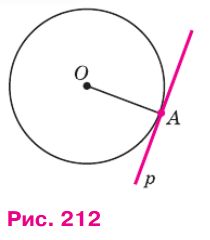
Пусть р — касательная к окружности с центром О, А — точка касания (см. рис. 212). Докажем, что касательная р перпендикулярна к радиусу ОА.
Предположим, что это не так. Тогда радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведённый из точки О к прямой р, меньше наклонной ОА, то расстояние от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки. Но это противоречит условию: прямая р — касательная.
Таким образом, прямая р перпендикулярна к радиусу ОА. Теорема доказана.
Сообщить об ошибке
Сообщитe об ошибке