ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 5 стр. 133
Условие
Сформулируйте и докажите теорему о вычислении площади параллелограмма.
Решение #1
Теорема:
Площадь параллелограмма равна произведению его основания на высоту.
Доказательство:
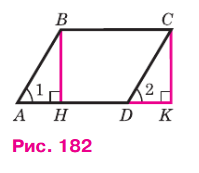
Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD за основание и проведём высоты ВН и СK (рис. 182). Докажем, что S = AD ⋅ BH.
Докажем сначала, что площадь прямоугольника НВСK также равна S. Трапеция ABСK составлена из параллелограмма ABCD и треугольника DCK. С другой стороны, она составлена из прямоугольника НВСK и треугольника ABН. Но прямоугольные треугольники DCK и ABН равны по гипотенузе и острому углу (их гипотенузы AB и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых AB и CD секущей AD), поэтому их площади равны.
Следовательно, площади параллелограмма ABCD и прямоугольника НВСK также равны, т. е. площадь прямоугольника НВСK равна S. По теореме о площади прямоугольника S = BC ⋅ BH, а так как BC = AD, то S = AD ⋅ BH. Теорема доказана.
Сообщить об ошибке
Сообщитe об ошибке