ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 51 стр. 21
Условие
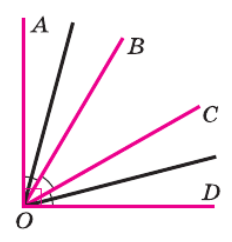
На рисунке 38 угол AOD — прямой, ∠AOB = ∠BOC = ∠COD. Найдите угол, образованный биссектрисами углов AOB и COD.
Решение #1
Поскольку угол AOD прямой, его градусная мера равна 90°. Углы AOB, BOC и COD равны между собой, обозначим их градусную меру как x. Тогда:
x + x + x = 90°
3x = 90°
x = 30°
Каждый из углов AOB, BOC и COD равен 30°.
Пусть OE — биссектриса угла AOB, а OF — биссектриса угла COD. Тогда:
Угол EOF равен:
Таким образом, угол, образованный биссектрисами углов AOB и COD, равен 60°.
Сообщить об ошибке
Сообщитe об ошибке