ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 66 стр. 25

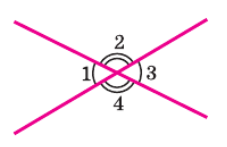
Давайте решим эту задачу, используя свойства углов, образующихся при пересечении двух прямых:

Вертикальные углы равны:

∠1 = ∠3

∠2 = ∠4

Смежные углы в сумме дают 180°:

∠1 + ∠2 = 180°

∠2 + ∠3 = 180°

∠3 + ∠4 = 180°

∠4 + ∠1 = 180°

Используем эти свойства для каждого случая:

a) ∠2 + ∠4 = 220°

1. Так как ∠2 и ∠4 – вертикальные углы, они равны: ∠2 = ∠4.

2. Подставим это в данное уравнение:

∠2 + ∠2 = 220°

2 * ∠2 = 220°

∠2 = 220° / 2

∠2 = 110°

3. Следовательно, ∠4 = 110°.

4. Углы ∠1 и ∠2 являются смежными, поэтому их сумма равна 180°:

∠1 + ∠2 = 180°

∠1 + 110° = 180°

∠1 = 180° — 110°

∠1 = 70°

5. Так как ∠1 и ∠3 – вертикальные углы, они равны: ∠3 = 70°

б) 3 (∠1 + ∠3) = ∠2 + ∠4

1. Используем свойство вертикальных углов: ∠1 = ∠3 и ∠2 = ∠4.

2. Подставим это в уравнение:

3 * (∠1 + ∠1) = (∠2 + ∠2)

3 * (2 * ∠1) = 2 * ∠2

6 * ∠1 = 2 * ∠2

3. Разделим обе части на 2:

3 * ∠1 = ∠2

4. Углы ∠1 и ∠2 являются смежными, поэтому их сумма равна 180°:

∠1 + ∠2 = 180°

5. Подставим выражение для ∠2 (3 * ∠1) в это уравнение:

∠1 + (3 * ∠1) = 180°

4 * ∠1 = 180°

∠1 = 180° / 4

∠1 = 45°

6. Следовательно, ∠3 = 45°.

7. Найдем ∠2:

∠2 = 3 * ∠1 = 3 * 45°

∠2 = 135°

8. Следовательно, ∠4 = 135°.

в) ∠2 − ∠1 = 30°

1. У нас есть система из двух уравнений:

∠2 − ∠1 = 30° (дано)

∠2 + ∠1 = 180° (смежные углы)

2. Сложим эти два уравнения:

(∠2 − ∠1) + (∠2 + ∠1) = 30° + 180°

2 * ∠2 = 210°

∠2 = 210° / 2

∠2 = 105°

3. Следовательно, ∠4 = 105°.

4. Подставим значение ∠2 в уравнение ∠2 + ∠1 = 180°:

105° + ∠1 = 180°

∠1 = 180° — 105°

∠1 = 75°

5. Следовательно, ∠3 = 75°.