ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 67 стр. 25
Условие
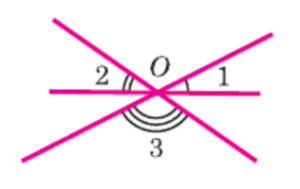
На рисунке 47 изображены три прямые, пересекающиеся в точке О. Найдите сумму углов: ∠1 + ∠2 + ∠3.
Решение #1
1. Вертикальные углы:
Угол, расположенный между двумя наклонными прямыми над горизонтальной прямой, является вертикальным по отношению к углу ∠3. Поскольку вертикальные углы равны, этот угол также равен ∠3.
2. Углы на прямой:
Углы, лежащие на одной стороне прямой и образующие ее, в сумме дают 180°.
На горизонтальной прямой, с ее верхней стороны, расположены три угла:
- ∠1 (угол между горизонтальной прямой и правой наклонной прямой)
- Угол, вертикальный углу ∠3 (угол между двумя наклонными прямыми)
- ∠2 (угол между горизонтальной прямой и левой наклонной прямой)
3. Сумма углов:
Следовательно, сумма этих трех углов равна 180°:
∠1 + (угол, вертикальный ∠3) + ∠2 = 180°
Поскольку угол, вертикальный ∠3, равен самому ∠3, мы можем заменить его:
∠1 + ∠3 + ∠2 = 180°
Сообщить об ошибке
Сообщитe об ошибке