ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 68 стр. 25

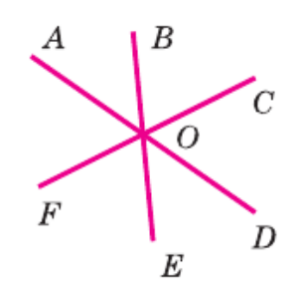
1. Найдем ∠BOC:

Углы ∠BOC и ∠FOE являются вертикальными углами (образованы пересечением прямых BE и FC).
Следовательно, ∠BOC = ∠FOE = 70°.

2. Найдем ∠DOE:

Углы ∠AOB и ∠DOE являются вертикальными углами (образованы пересечением прямых AD и BE).
Следовательно, ∠DOE = ∠AOB = 50°.

Теперь приступим к нахождению требуемых углов:

а) Найдите ∠AOC:

Угол ∠AOC состоит из суммы углов ∠AOB и ∠BOC.

∠AOC = ∠AOB + ∠BOC

∠AOC = 50° + 70°

∠AOC = 120°

б) Найдите ∠BOD:

Угол ∠BOD является смежным с углом ∠AOB на прямой AD (так как A, O, D лежат на одной прямой).
∠AOB + ∠BOD = 180° (это неверно, AOB и BOD не смежные на прямой AD, т.к. B не лежит на AD)

Рассмотрим углы на прямой AD: ∠AOC и ∠COD — смежные углы.

∠COD = 180° — ∠AOC = 180° — 120° = 60°.

Теперь найдем ∠BOD. Он состоит из углов ∠BOC и ∠COD.

∠BOD = ∠BOC + ∠COD

∠BOD = 70° + 60°

∠BOD = 130°

Альтернативный способ для ∠BOD:

Углы ∠AOE и ∠BOD являются вертикальными углами (образованы пересечением прямых AD и BE).

Чтобы найти ∠AOE, нам нужно найти ∠AOF.

Углы ∠AOF и ∠COD являются вертикальными углами (образованы пересечением прямых AD и FC)

Мы нашли ∠COD = 60°, значит ∠AOF = 60°.

Теперь ∠AOE = ∠AOF + ∠FOE = 60° + 70° = 130°.

Так как ∠BOD = ∠AOE, то ∠BOD = 130°. (Этот способ подтверждает результат).

в) Найдите ∠COE:

Углы ∠BOC и ∠COE являются смежными углами на прямой BE.

∠BOC + ∠COE = 180°

70° + ∠COE = 180°

∠COE = 180° — 70°

∠COE = 110°

Альтернативный способ для ∠COE:

Углы ∠COE и ∠BOF являются вертикальными углами (образованы пересечением прямых BE и FC).

Углы ∠FOE и ∠BOF являются смежными углами на прямой FC.

∠FOE + ∠BOF = 180°

70° + ∠BOF = 180°

∠BOF = 180° — 70° = 110°.

Следовательно, ∠COE = 110°. (Этот способ подтверждает результат).

г) Найдите угол между прямыми AD и FC:

Прямые AD и FC пересекаются в точке O, образуя углы:

∠AOC = 120°

∠COD = 60° (смежный с ∠AOC)

∠DOF = 120° (вертикальный с ∠AOC)

∠AOF = 60° (вертикальный с ∠COD)

Угол между двумя прямыми обычно определяется как наименьший из образовавшихся углов (острый угол). В данном случае, это 60°.