ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 7 стр. 133
Условие
Сформулируйте и докажите теорему об отношении площадей двух треугольников, имеющих по равному углу.
Решение #1
Теорема:
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Доказательство:
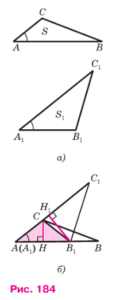
Пусть S и S1 — площади треугольников ABC и A1B1C1, у которых ∠A = ∠A1 (рис. 184, а). Докажем, что
S/S1=AB*AC/A1B1*A1C1
Наложим треугольник А1В1С1 на треугольник ABC так, чтобы вершина A1 совместилась с вершиной А, а стороны А1B1 и А1С1 наложились соответственно на лучи AB и АС (рис. 184, б). Треугольники ABC и AB1C имеют общую высоту СН, поэтому S/SAB1C=AB/AB1. Треугольники AB1C и AB1C1 также имеют общую высоту — В1H1, поэтому SAB1C/SAB1C1=AC/AC1. Перемножая полученные ра-венства, находим:
SAB1C/SAB1C1=AB*AC/AB1*AC1 или S/S1=AB*AC/A1B1*A1C1
Теорема доказана.
Сообщить об ошибке
Сообщитe об ошибке