ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 718 стр. 186
Условие
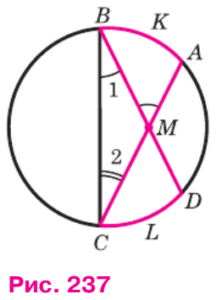
По данным рисунка 237 докажите, что
∠AMB = 1/2(U CLD + U AKB).
Решение #1
1. Проведем хорду BC. Это добавит в рисунок треугольник BMC.
2. ∠AMB – внешний угол треугольника BMC. Внешний угол треугольника равен сумме двух противоположных внутренних углов. Поэтому:
∠AMB = ∠MBC + ∠BCM (∠AMB = ∠1 + ∠2)
3. Теорема о вписанном угле. Теорема гласит, что вписанный угол равен половине дуги, на которую он опирается. Применим эту теорему к углам ∠1 и ∠2:
∠1 = 1/2 дуги CLD (угол ∠1 опирается на дугу CLD)
∠2 = 1/2 дуги AKB (угол ∠2 опирается на дугу AKB)
4. Подставим выражения для ∠1 и ∠2 в уравнение из шага 2:
∠AMB = 1/2 (U CLD + U AKB)
Сообщить об ошибке
Сообщитe об ошибке