ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 95 стр. 31

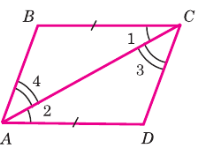
а) Для доказательства равенства треугольников мы можем использовать один из признаков равенства (по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трём сторонам, или по стороне и двум углам).

Рассмотрим треугольники ABC и CDA:

1. BC = AD (дано в условии, и отмечено одинарными штрихами на рисунке).

2. ∠1 = ∠2 (дано в условии, и отмечено двойными дугами на рисунке. ∠1 это ∠BCA, а ∠2 это ∠CAD).

3. AC = CA (общая сторона для обоих треугольников).

Теперь посмотрим на признак равенства по двум сторонам и углу между ними:

В ΔABC у нас есть сторона BC, угол ∠BCA (∠1) и сторона AC.

В ΔCDA у нас есть сторона AD, угол ∠CAD (∠2) и сторона CA.

Мы видим, что:

• BC = AD (сторона)
• ∠BCA = ∠CAD (угол, заключенный между этими сторонами)
• AC = CA (сторона)

Таким образом, по первому признаку равенства треугольников (по двум сторонам и углу между ними), треугольник ABC равен треугольнику CDA.

б) Так как мы доказали, что треугольник ABC равен треугольнику CDA, то их соответствующие стороны и углы равны.

Соответствующие стороны:

• BC соответствует AD (дано, что они равны).
• AB соответствует CD.
• AC соответствует CA (общая сторона).

Мы знаем, что: AD = 17 см и DC = 14 см

Из равенства треугольников следует:

• BC = AD (соответствующие стороны). Так как AD = 17 см, то BC = 17 см.
• AB = DC (соответствующие стороны). Так как DC = 14 см, то AB = 14 см.