ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 96 стр. 31
Условие
На рисунке 54 OA = OD, OB = OC, ∠1 = 74°, ∠2 = 36°. а) Докажите, что треугольники AOB и DOC равны; б) найдите ∠ACD.
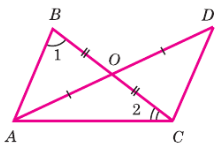
Решение #1
б) В пункте а) мы доказали, что треугольник AOB равен треугольнику DOC (ΔAOB = ΔDOC) по двум сторонам и углу между ними: OA=OD, OB=OC, и вертикальные углы ∠AOB = ∠DOC).
Из равенства этих треугольников следует, что их соответствующие углы равны:
∠OAB (или ∠BAO) = ∠ODC (или ∠CDO)
∠OBA (или ∠ABO) = ∠OCD (или ∠DCO)
Теперь посмотрим на данные в задаче:
∠1 = 74°, и по рисунку это ∠ABC (то есть ∠ABC=∠OCD = 74° как вертикальные).
∠2 = 36°, и по рисунку это ∠ACD.
Угол ∠ACD состоит из двух частей: ∠ACO и ∠OCD.
∠ACD = ∠ACO + ∠OCD
Мы знаем, что ∠OCD = ∠1 = 74° и ∠ACO=36°.
∠ACD = ∠ACO + ∠OCD
∠ACD = 74° + 36°
∠ACD = 110°
Сообщить об ошибке
Сообщитe об ошибке